Una empresa local de Tecnología desarrolla en tiempo record un chatbot que alimentado con una secuencia de lógica de respuestas a través de WhatsApp o vía web, realiza un test rápido con preguntas para identificar si las personas pudieran padecer síntomas del Coronavirus, de confirmar que los síntomas corresponden al virus el chatbot tiene la capacidad de derivar el paciente a una consulta médica por videoconferencia para validar con un especialista si realmente estaría contagiado y recibe el paciente instrucciones para proceder informado a iniciar su cuarentena y toda las información colectada sirve para detectar y geolocalizar la evolución de la epidemia, lo que ayudaría a enfocar los esfuerzos para combatir el desarrollo de la enfermedad alimentando con datos en tiempo real la evolución de la epidemia, ¿realidad o fantasía? Pues realidad y está sucediendo ahora.
Desde el inicio de la hoy ya Pandemia conocida mundialmente como COVID-19 se ha desarrollado una carrera para poder encontrar una solución en la forma de vacuna o de tratamientos efectivos y desde distintos frente se ha trabajado no quedando exentas de ella las Herramientas de Inteligencia Artificial articuladas en el dedicado trabajo de los laboratorios que con sus equipos de Científicos de Datos analizan diariamente montañas de datos generando modelos dinámicos para entender el comportamiento del virus, descifrar su genoma y predecir su evolución.
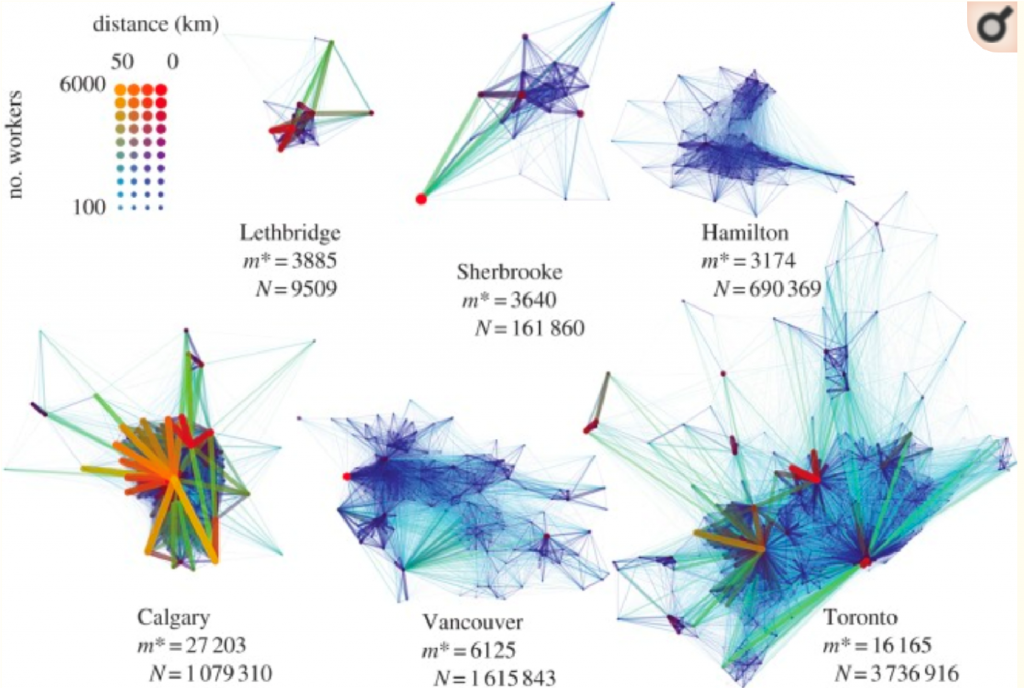
Se han desarrollado una serie de modelos dinámicos basados en Machine Learning e Inteligencia Artificial analizando datos de las acciones estudiadas del movimiento de trabajadores en las ciudades los que apuntan a enfocar el problema desde la visión de las estructuras de propagación según como se desplazan individuos con distintas necesidades por la ciudad que también son empleados para entre otras cosas definir tramos censales que permitan establecer mediante una muestra el comportamiento de las distintas fases epidémicas, los escenarios que se darán enfocándose en el movimiento o desplazamientos de los individuos en una zona metropolitana para determinar cómo y de qué manera será efectiva aplicar una medida como una cuarentena y cómo distribuir en forma efectiva los recursos que estén dispuesta en una determinada zona (Dalziel, Benjamin D Pourbohloul, Babak and Ellner ,Stephen P. 2013)
Patrones de movilidad de los trabajadores en las ciudades. El grosor y el color de los bordes muestran el número de personas que viajan entre Secciones Censales (SC). Los círculos son en realidad bordes cortos, que representan individuos que viven y trabajan en la misma SC. Las ciudades más grandes tienden a tener patrones de transporte más organizados, medidos por el número promedio de trabajadores que tienen su estación de trabajo en la misma SC que un trabajador elegido al azar (m *). Sin embargo, las ciudades también muestran marcadas diferencias en la organización que son independientes del tamaño de la población.
Analicemos un Modelo evolutivo
SIR modelo matemático que describe tres curvas modelando primero la población susceptible de ser infectada pero que aún no se infecta, segundo los infectados y finalmente los que se recuperan. Todo esto ajustado en función del tiempo transcurrido.
El modelo SIR describe el cambio en la población de cada uno de estos compartimientos en términos de dos parámetros, β y γ. β describe la tasa de contacto efectiva de la enfermedad: un individuo infectado entra en contacto con βN otros individuos por unidad de tiempo (de los cuales la fracción que es susceptible a contraer la enfermedad es S / N). γ es la tasa de recuperación media: es decir, 1 / γ es el período de tiempo medio durante el cual un individuo infectado puede transmitirlo.
Las ecuaciones diferenciales que describen este modelo fueron derivadas primero por Kermack y McKendrick [Proc. R. Soc. A, 115, 772 (1927)]
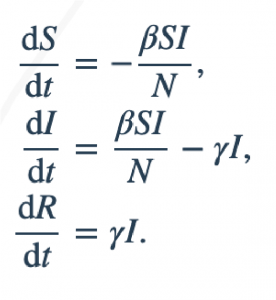
Codificando con Python un modelo
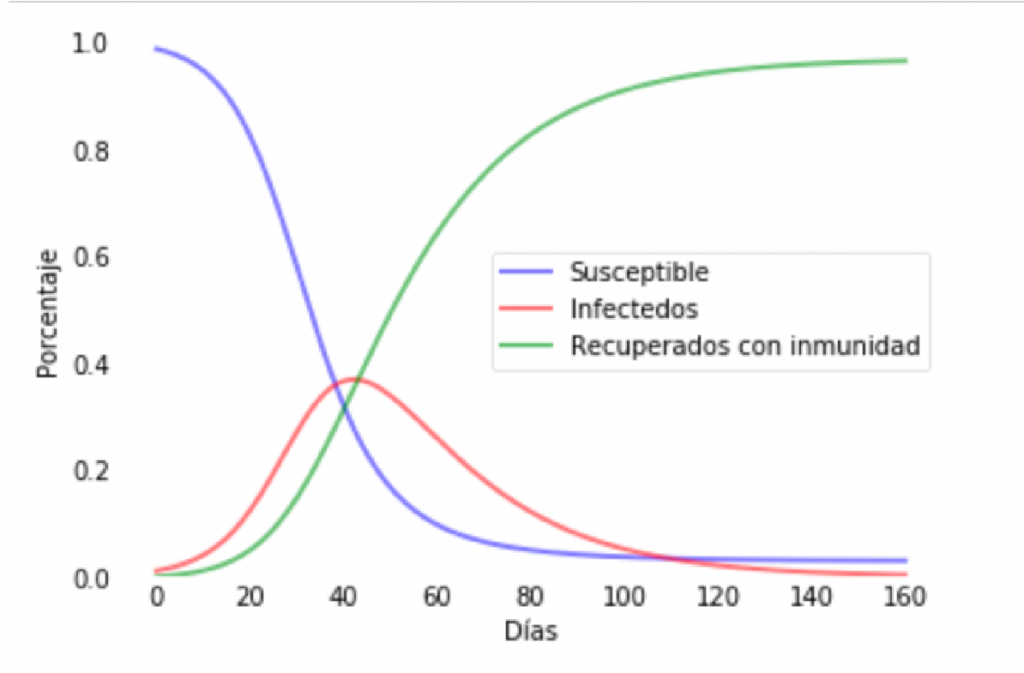
El siguiente código de Python integra estas ecuaciones para una enfermedad caracterizada por los parámetros β = 0.2, 1 / γ = 10 días en una población de N = 500 (quizás ‘gripe en una escuela). El modelo se inicia con una sola persona infectada el día 0: I (0) = 1. Las curvas trazadas de S (t), I (t) y R (t) están diseñadas para verse un poco mejor que los valores predeterminados de Matplotlib.
import numpy as np from scipy.integrate import odeint
import matplotlib.pyplot as plt
# Población Total, N.
N = 500
# Número inicial del Infectados y Recuperados (Inmmunes), I0 y R0.
I0, R0 = 1, 0
# Todos ademas , S0, son sujetos suceptibles de ser infectados S0 = N - I0 - R0
# Contact rate, beta, and mean recovery rate, gamma, (in 1/days). beta, gamma = 0.18, 1./10 # A grid of time points (in days)
t = np.linspace(0, 160, 160)
# Modelo SIR ecuaciones diferenciales. def deriv(y, t, N, beta, gamma):
S, I, R = y
dSdt = -beta * S * I / N dIdt = beta * S * I / N - gamma * I
dRdt = gamma * I return dSdt, dIdt, dRdt # Vector de condiciones iniciales.
y0 = S0, I0, R0
# Ecuaciones integadas de SIR sobre la grilla de tiempos, t. ret = odeint(deriv, y0, t, args=(N, beta, gamma))
S, I, R = ret.T
# Ploteo de tres curvas separadas
S(t), I(t) y R(t) fig = plt.figure(facecolor='w') ax = fig.add_subplot(111, axisbelow=True) ax.plot(t, S/N, 'b', alpha=0.5, lw=2, label='Susceptible') ax.plot(t, I/N, 'r', alpha=0.5, lw=2, label='Infectados')
ax.plot(t, R/N, 'g', alpha=0.5, lw=2, label='Recuperados con inmunidad') ax.set_xlabel('Días') ax.set_ylabel(‘Porcentaje') ax.set_ylim(0,1)
ax.yaxis.set_tick_params(length=0) ax.xaxis.set_tick_params(length=0) ax.grid(b=True, which='major', c='w', lw=2, ls='-') legend = ax.legend() legend.get_frame().set_alpha(0.5) for spine in ('top', 'right', 'bottom', 'left'): ax.spines[spine].set_visible(False) plt.show()
Son muchas las formas que la ciencia de datos hoy puede aportar en entregar a la contingencia generada por el Covid-19 herramientas para tomar decisiones y ayudar con las acciones que las autoridades que están a cargo, ¿Será esta crisis una oportunidad para lo que se definió el trabajo más sexy y cool del siglo 21?
Perfil del autor
- Fernando Fajardo
- Trabajó en desarrollar la Innovación y las Tecnologías en la Educación. Estoy por Promover el conocimiento en el uso de las tecnologías, orientando a las organizaciones en la adopción de nuevos modelos de gestión empleando tecnologías, incorporando nuevos paradigmas en la gestión de tecnologías en Docencia e Investigación. Colaborando con las organizaciones de educación para facilitar procesos de adopción de nuevas tecnologías.




